Musik und Mathematik

Musik ist empfundene, verzeitlichte, hörbare Mathematik, man könnte auch sagen: Ein Faß ohne Boden. Einmal getriggert, kann man sich unendlich lange verlaufen, verirren und verrechnen. Ein faszinierendes Feld mit einer Fülle praktischer Empfehlungen für Musiker und Therapeuten. Hier erwartet Sie eine hochvernetzte Seite zu ausgesuchten Quellen rund um das duale Universum von Musik und Mathematik:

Die zwei untrennbaren Geschwister

Musik ist empfundene, verzeitlichte, hörbare Mathematik, schreibt Hans Zimmermann und belegt es akribisch, sozusagen bis auf das Komma genau. Damit steht er nicht allein: Hunderte von mehr oder weniger kompetenten Quellen und Autoren (und eine Reihe von Nobelpreisträgern) halten es genauso. Schließlich sind Musik und Mathematik wie zwei Geschwister: Mal drängt sich die eine vor, mal der andere.

Die enge Verwandschaft zwischen Musik und Mathematik ist in den Zeiten digitaler Klangverarbeitung offenkundig, doch schon Pythagoras wußte ein Lied davon zu singen.

Für Barockmusikern wie J.S. Bach war Musik stets (auch) ein Spiel mit Zahlen und Regeln, Serien und Intervallen, Korrelationen und Ordnungen (SWR2 (Vom Innen und Aussen der Klänge). Es gibt es eine Reihe spannender und tiefgehender Websites darüber, eine Reihe Softwaretools zur Musikproduktion by Numbers, off- und online.

Hier einige Basics zum Thema, geballte Link Power mit zahlreichen praktischen Möglichkeiten zur Umsetzung mathematischer und musikalischer Natur, faszinierenden Ausflügen in entfernte Fachgebiete, wobei die Bilder jewils mit den Zahlen übereinstimmen, one, two, three, four ...

Die Fibonacci-Reihe

Eine weitere große Konstante in der Natur: Kaninchen vermehren sich entlang der Fibonacci-Reihe, Tannenzapfen und Sonneblumen, Mozart und Bach spielten und komponierten mit ihr, kurz die Fibonacci-Reihe ist ein (musikalischer) Klassiker, eine Konstante in der Natur, auf die man zählen und die man folglich auch in Töne giessen kann, was immer wieder Generationen von Musikern fasziniert.

Zum besseren Verständnis der musikalischen Mathematik hier einige Artikel zum Thema. Einen fundierten Überblick bietet die Arbeit einer Jugend forscht Teilnehmerin, Corinna Brinkmann, ein Beitrag über Fibonacc-Kurven an der Börse, das entsprechende Softwareprogramm und das passende Buch (Noten und Banknoten).

Primzahlen - Grundlage der Musik?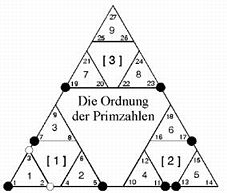

Die Primzahlen spielen eine geheimnisvolle Rolle in der Mathematik - und der Musik. Graf Arnold Keyserling hat damit experimentiert, aber auch die Aphex Twins und natürlich Frickers, der "von den Verhältniszahlen der Intervalle ausgeht, wie sie sich an einem Monochord abnehmen lassen (die Saitenlängen verhalten sich umgekehrt proportional zu den hörbaren Schwingungen).

Dabei bemerkt er, daß sich sämtliche Verhältnisse auf die ersten drei Primzahlen 2, 3 und 5 zurückführen lassen und diese somit die eigentliche Grundlage der Musik bilden. Alle Primzahlen, die 5 überschreiten, gelten ihm einschließlich der aus ihnen ableitbaren Verhältnisse als "gänzlich zur Musik in der uns bekannten Natur unbrauchbar". Die amtliche Website für Musik und Primzahlen: Aesthetics of the Prime Sequence.

Pi in der Musik

Die Regel vom Goldenen Schnitt besagt, dass sich der kürzere Abschnitt zum längeren so verhalten sollte, wie der Längere zur Summe aus Kürzerem und Längerem. Dieses Verhältnis empfinden wir als besonders ästhetisch, es findet sich in den Proportionen des Menschen, in der Malerei, der Architektur - und in der Musik, wofür es zahlreiche Ansätze gibt ***, siehe PHI HARMONIC.

Linkempfehlung: Was ist Musik?
"Musik ist empfundene, verzeitlichte, hörbare Mathematik", schreibt Hans Zimmermann und zeigt auf seiner Webseite auf, was er darunter versteht - und das ist eine ganze Menge! Nachdrückliche Empfehlung: Was ist Musik?

In der fractalen Mathematik gilt er als "letzte Bastion der Ordnung im Chaos" und der Biologe Hans Paul van den Haag hat Übereinstimmung in der Nucleotidsequenz (a,c,g,t) eines Fisches (Torpedo Torpedo) mit der Zahl PI zur Basis 4 bis auf 193 Stellen festgestellt! (Spektrum der Wissenschaft 4/1996 S.23). Solche und andere Meldungen tauchen immer wieder auf - und belegen nicht nur die Liebe der Mathematiker zu Zahlenspielen, sondern auch die Häufigkeit bestimmter mathematischer Strukturen in der Natur.

Fractale Musik

Fractale Mathematik, Chaostheorie und Apfelmännchen gehören zu den urbanen Mythen, ebenso, daß der Flügelschlag eines Schmetterlings in China in den Anden ein Erdbeben auslösen kann. Also, immer wenn ein Sack Reis umfällt ...

In der fraktalen Musik treffen Chaos und Ordnung, Zufall und Vorhersehbarkeit munter aufeinander - wie in der richtigen Welt. Die lästige (und ohne Computer nicht realisierbare) Rechnerei übernimmt inzwischen fraktale Musiksoftware, auf MP3.com gibt es interessante fractale Seite und auch hierzulande gibt es überraschende Musik (KlangKreativ, Stichwort "weitere"). Und wer sich für fractale Software interessiert, auf der Website des RANDOM MUSIC for Y2K PROJECT wird eine Reihe fractaler Programme überraschend präsentiert und aufgelistet. Ebenfalls repräsentativ, wenn auch (bei der Software) mit vielen toten Links: Das FRACTAL MUSIC LAB mit zahlreichen Infos, Manuals, Files, Programmbeispielen und Foren.

Gold wert für Musiker:
Akkord und Rhythmus

Was passiert, wenn Tonhöhe und Rhythmus in einem harmonischen, kohärenten Verhältnis zueinander stehen? Stephen Jay fan einen ganz eigenen, hitverdächtigen Zugang dazu, mehr über "Harmonic Rhythm" auf seiner Website und konzeptionell hier in den nächsten Tagen. Table 1-4: Pitch/Pulse Conversion for "A" 110

			(bmp)	(cps)
		Original Pitch	6600.00	110.00
		1 octave down-	3300.00	55.00
		2 octaves down-	1650.00	27.50
		3 ocataves down-	825.00	13.75
		4 ocataves down-	412.50	6.87
	Presto	5 ocataves down-	206.25	3.43
{Rhythmic range}	Allegro	6 ocataves down-	103.12	1.71 1
	Largo	7 ocataves down-	51.56	.85

An understanding of the rhythmic basis for harmonic sonorities can aid in the overall integration of the components of music. For example a tempo, when viewed as tonic, can be chosen accordingly. The key of "C" for example would have the greatest degree of harmo-rhythmic "sympathy" at 61,123, or 246 beats per minute.

Performance techniques can synchronize, offset or fragment harmo-rhythmicity. Arppegiations can be played in time with the harmo-rhythmics to create desirable combinatory tones. Certain scale temperings, timbre voicings, interval bending, and off-sets produce unusually perfect harmo-rhythms. Bending notes and glissandos equal ritards and accelerandos on the harmo-rhythmic level. When relative synchronization is performed, and the frequency of the dominant pitches are multiples of the tempo and rhythm at which they are being played, a wide natural resonance occurs between the most basic aspects of music. Table 1-5, Sympathetic Tempo

KEY	CPS	FAST	MEDIUM	SLOW	(BPM)
A	110	206	103	52
A#	117	219	109	55
B	123	230	115	58
C	131	246	123	61
C#	139	260	130	65
D	147	275	137	68
D#	156	292	146	73
E	165	309	154	77
F	175	328	164	82
F#	185	346	173	86
G	196	367	183	91
G#	208	390	195	97

---

Stephen Jay: Harmonic Rhythm